
RESEARCH
Ultrafast quantum simulators and computers with ultracold Rydberg atoms
We take the ultrafast coherent control technique with attosecond precision developed in our previous research lines (wave-packet interferences in molecules and bulk solids) and apply it to a completely different object, ultracold Rydberg atoms, to develop a new type of Rydberg quantum simulators and computers.
Rydberg atoms are any atom with a valence electron put in a highly-excited orbital (large principal quantum number n). This dramatically enlarges the size of the electronic wavefunction (scaling as n2) from the Bohr radius (0.05 nm) to ~100 nm and more. The electric dipole formed by this far-orbiting Rydberg electron and the core nucleus is similarly enhanced, leading to sizable dipole-dipole interactions between two Rydberg atoms. Atoms separated by a few micrometers now feel each other! The interaction can be controlled by tuning the Rydberg level or the microscopic distance between the atoms.
Ultracold refers to the extreme control that we gain on the position and velocity of atoms using state-of-the-art techniques of laser cooling and trapping. Because the dipole-dipole interaction between atoms is so sensitive to their distance, we want to control this degree of freedom as much as allowed by quantum physics. Using traps made of light (optical lattice or tweezers), we pin the atoms position and then remove thermal fluctuations by cooling atoms down to the quantum regime. After removing all quanta of motions, atoms are confined to the bottom of the traps and only subject to tiny (~10s of nm) quantum fluctuations.
Ultrafast describes how we excite atoms to Rydberg states. The Rydberg atom community have mainly been using cw (continuous-wave) lasers to bring the valence electron up to the Rydberg level. Because this transition is so hard to drive (the wavefunctions of the ground and Rydberg electron having so little overlap) and due to the limited power of cw lasers, the excitation is typically completed in a timescale of ~0.1 microsecond. While fast compared to the 100 μs lifetime of a Rydberg electron, it remains 10 000 times slower than the 10 ps radial period (defined by the energy separation between Rydberg orbits), which sets the speed limit at which a well-identified Rydberg state can be prepared. Using pulsed laser technology to concentrate the laser power in a picosecond pulse, we close this gap and realize ultrafast excitation of Rydberg states. In fact, our pulses being initially shorter than the orbit period (we can make them longer by spectral shaping), we can even excite a superposition of Rydberg states forming a Rydberg wave packet! Going ultrafast allows us to explore new exciting directions with strongly interacting Rydberg atoms.
Ultrafast and ultracold Rydberg quantum simulators and computers
Combining the above techniques and ideas, we explore new regimes of quantum physics. This challenges us with a variety of questions and problems ranging from very technical ones to more fundamental concepts:
- How fast can we bring atoms to a single Rydberg state? How could we use and think about Rydberg wave packets? Can we develop more powerful and stable pulsed lasers for the excitation?
- How close can we controllably bring two atoms together with optical tweezers? How can we further squeeze the atoms localization in their trap after having removed all thermal fluctuations?
- Can we excite atoms which are so close that their Rydberg electrons overlap? And what happens to these Rydberg electrons afterwards? Could the Rydberg electrons delocalize over an atomic array in the same way than in a metal?
- How fast can two atoms interact together and generate entanglement? How precisely can we control this entanglement? Can we make an ultrafast quantum gate out of it?
- How can we observe and model the dynamics of many (2, 3, ~10000s) interacting Rydberg atoms?
- Can our ultrafast quantum simulator be extended to a scalable / high-coherence quantum computer (adiabatic / gate-based)?
- …
To answer these questions, we have been developing three Generations of experimental setups: 1G, 2G and 3G, all using our good-old Rubidium 87 atom.
[ 1st Generation: 1G ]
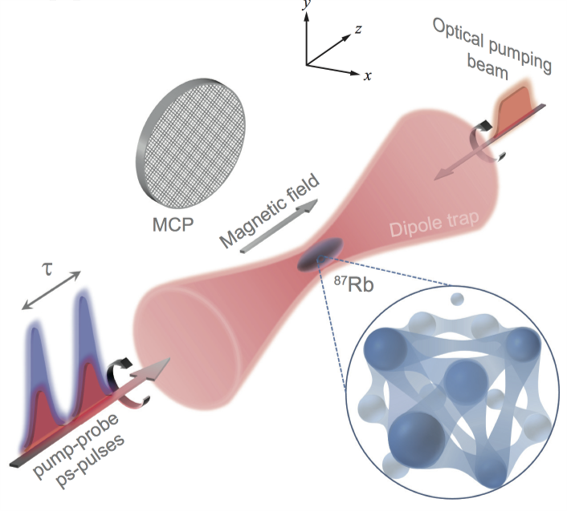
| Figure 1. Schematic of the 1G system: the atoms in the optical dipole trap are excited to a Rydberg state with pulse lasers. The figure is adopted from Ref. [1]. |
In 1G (decommissioned), the 87Rb atoms are cooled in a magneto-optical trap and loaded into a large optical dipole trap where they form a disordered atomic cloud with an average inter-atomic separation of 1 μm (Fig. 1). Here, ultrafast many-body electron dynamics in a strongly correlated ultracold Rydberg gas has been observed and controlled on the attosecond timescale by ultra-precise coherent control [1].
[ 2nd Generation: 2G ]
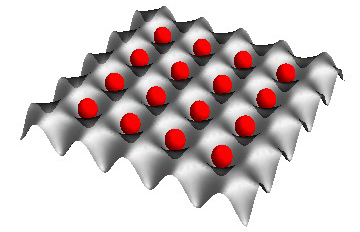
| Figure 2. Schematic of the unit filling Mott insulator. Single atoms are trapped in each site in an optical lattice. |
In 2G, we go a step beyond and prepare ordered atomic arrays of up to 30 000 ultracold atoms making a 532 nm cubic lattice (Fig. 2. our first observation in 2016) by preparing a unit-filling Mott insulator (Fig. 3. our first observation in 2016) with a BEC (Fig. 4. our first observation in 2015) loaded into an optical lattice. We also developed a theoretical model which describes the many-body dynamics of the strongly correlated Rydberg gas in a dipole trap as well as in an optical lattice [2].
| Figure 3. Absorption images of the atomic cloud at different lattice depths, taken after 15 ms free expansion. |

| Figure 4. Absorption images of the atomic cloud at different stages of the evaporative cooling, taken after 20 ms free expansion. |
[ 3rd Generation: 3G ]
In 3G, we build things atom by atom, creating arrays ranging from 1 to 1000 microscopic optical tweezers each holding a single laser-cooled 87Rb atom (Fig. 5, 6). The tweezers array can be modified at will to generate any arrangements of the atoms, with inter-atomic distance down to ~1 μm, and with single-atom addressing.
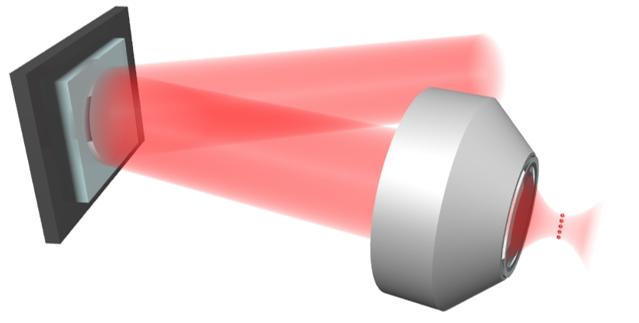
| Figure 5. Schematic of the optical tweezers system. We can generate an arbitrary-shape array of the tweezers and trap individual atoms by focusing the laser after controlling the wavefront and imprinting a hologram using a spatial light modulator. |
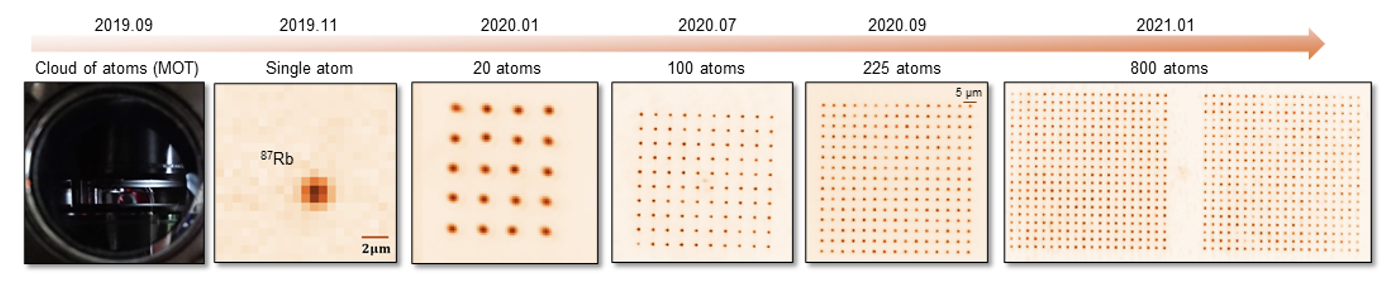
| Figure 6.Fluorescence imaging of the atoms trapped in optical tweezers array. Each dot corresponds to a single atom in the optical tweezers. |
Coherent Control, Information Processing, and Quantum/Classical Boundary
Coherent control is based on manipulation of quantum phases of wave functions. It is a basic scheme of controlling a variety of quantum systems from simple atoms to nanostructures with possible applications to novel quantum technologies such as bond-selective chemistry and quantum computation. Coherent control is thus currently one of the principal subjects of various fields of science and technology such as atomic and molecular physics, solid-state physics, quantum electronics, and information science and technology. We have developed high-precision wave-packet interferometry by stabilizing the relative quantum phase of two molecular wave packets on the attosecond time scale [1-5]. We have also succeeded in tailoring and visualizing spatiotemporal images of such wave-packet interference on the picometer and femtosecond scales as shown in Fig. 7 [3-8].
We are now tackling the following three projects by making use of these techniques.

| Figure 7. Actively tailored spatiotemporal images of quantum interference on the picometer and femtosecond scales. The relative phase of two vibrational wave-packets counterpropagating in the iodine molecule has been tuned to (a) 0, (b) 90, (c) 180, and (d) 270 degrees, respectively. Adopted from Ref. 3. |
Coherent control of bulk solids
For practical realization of a molecular computer and also exploring a mystery of quantum/classical boundary, we pursue the realization of coherent control of condensed matter systems. As long as coherent control is based on wave nature of matter, the quest to coherently control macroscopic objects would lead to verification of a mystery of wave/particle duality in the quantum world. By applying control schemes of quantum coherence, which could be obtained from our new quantum simulator, to real bulk solids, we are trying to realize coherent control of condensed matter systems. We already suceeded in optical manipulation of coherent phonons in superconducting YBa2Cu3O7-d thin films [9], and in optical engineering of quantum interference of delocalized wavefunctions in solid para-hydrogen as shown in Fig. 8 [10]. We have also succeeded in all optical control and visualization of ultrafast two-dimensional atomic motions in a single crystal of bismuth [11].
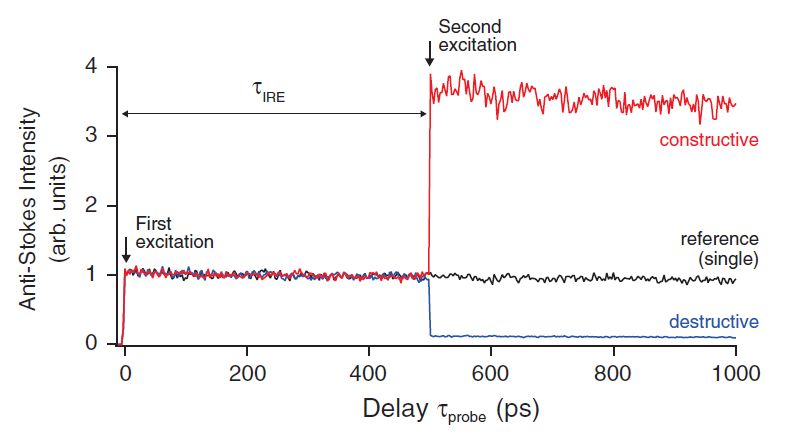
| Figure 8. Real-time observation of the actively controlled quantum interference of the vibron state delocalized in solid p-H2. The delay tIRE between the first and second laser pulse pairs is different by 4 fs between the red and blue traces [10]. |
Information processing with molecular wave functions
Our high-precision spatiotemporal coherent-control is applied to information processing with molecular wave functions [12,13]. We succeeded in discrete Fourier transfomation with a single 0.3-nanometer-size molecule, and the execution time was about 150 fs, which is 1000 times faster than the current fastest supercomputer [12]. To implement universal logic gates, we also demonstrated that a strong non-resonant fs laser pulse in the near-infrared region can modulate the population of each eigenstate within a molecular wave-packet (WP) [13]. This result has another interesting aspect. In quantum mechanics different eigenstates are orthogonal and do not interfere with each other, but we demonstrated that unusual interference among multiple quantum waves in different eigenstates is induced actively and controlled with a strong fs laser pulse. This new concept, which we refer to as "strong-laser-induced interference" is not specific to the molecular eigenstates, but universal to any type of eigenstates of a variety of quantum systems, being a new tool for quantum logic gates, and providing a new option to manipulate WPs with fs laser pulses in general applications of coherent control.
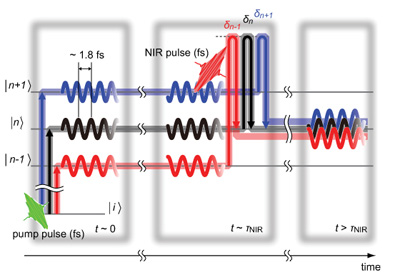
| Figure 9. Schematic of the strong-laser-induced interference. Starting from a common initial state, there are multiple quantum-mechanical pathways indicated by red, black, and blue lines, respectively, to the common final state. Those multiple pathways interfere quantum-mechanically with each other [13]. |
References
[1] N. Takei, C. Sommer et al., Nature Communications 7, 13449 (2016).
[2] C. Sommer et al., Phys. Rev. A 94,053607 (2016).
[3] H. Katsuki et al., Phys. Rev. Lett., 102, 103602 (2009).
[4] K. Ohmori, Annu. Rev. Phys. Chem. 60, 487-511 (2009).
[5] H. Katsuki et al., Phys. Rev. A 76,013403 (2007).
[6] K. Ohmori et al., Phys. Rev. Lett., 96, 093002 (2006).
[7] K. Ohmori et al., Phys. Rev. Lett., 91, 243003 (2003).
[8] H. Katsuki et al., Science 311, 1589-1592 (2006).
[9] Y. Okano et al., Faraday Discuss., 153, 375-382 (2011).
[10] H. Katsuki et al., Phys. Rev. B 88,014507 (2013).
[11] H. Katsuki et al., Nature Communications 4, 2801 (2013).
[12] K. Hosaka et al., Phys. Rev. Lett., 104, 180501 (2010).
[13] H. Goto et al., Nature Physics 7, 383-385 (2011).








