
NEWS
Generation of a unit-filling Mott insulator
We previously reported the generation of an 87Rb Mott insulator in a three-dimensional cubic optical lattice, in which each site was occupied by multiple atoms, so it was not ideal for our "ultrafast quantum simulator". This time we have successfully created and verified a unit filling (one atom per site) Mott insulator as follows.
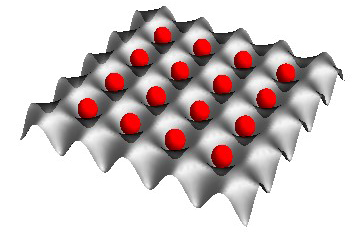
| Figure 1: Unit filling Mott insulator. |
Atom:
87Rb, 5S1/2, F=1
Methods:
We prepare an 87Rb BEC (F = 1, mF = 1) using a crossed-optical dipole trap (wavelength: 1064 nm). As forced evaporation proceeds, one can see the phase transition from thermal atoms to BEC in the momentum distribution (Fig. 2). Then we adiabatically load the BEC into a three-dimensional cubic optical lattice (wavelength: 1064 nm). As the final lattice depth increases, the quantum phase transition from BEC into Mott insulator via superfluid is visible in momentum distribution (Fig. 3), indicating the localization of atoms in each lattice site.
To control the filling of Mott insulator, we increased the lattice depth while decreasing the dipole-trap beam power to weaken the external trap confinement.
Simultaneously we apply magnetic field gradient to cancel out the gravity. A Mott insulator generated in the lattice is then irradiated with magneto-optical trap (MOT) beams (wavelength: 780 nm) [Fig. 4(a)].
During the irradiation period, atom pairs at multiply-occupied sites are lost due to inelastic light-assisted collisions, whereas the atoms at singly-occupied sites are lost more slowly by light-scattering loss.
The number of atoms that remain in the lattice after the irradiation is measured as a function of the irradiation time and the total initial number N of the atoms by absorption imaging.
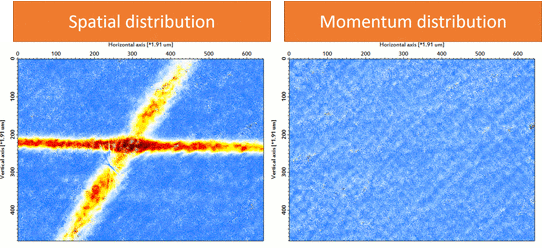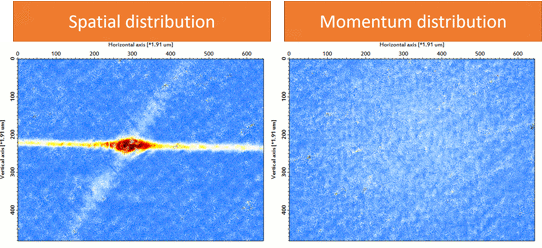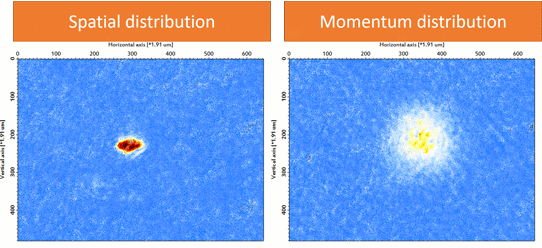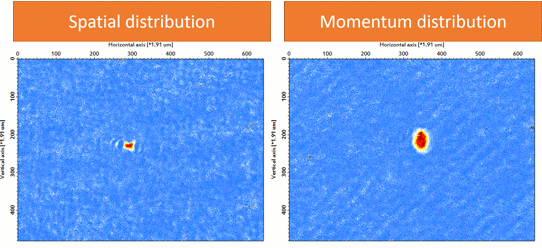
| Figure 2: Phase transition into Bose-Einstein Condensate (87Rb, F=1, mF=1). |
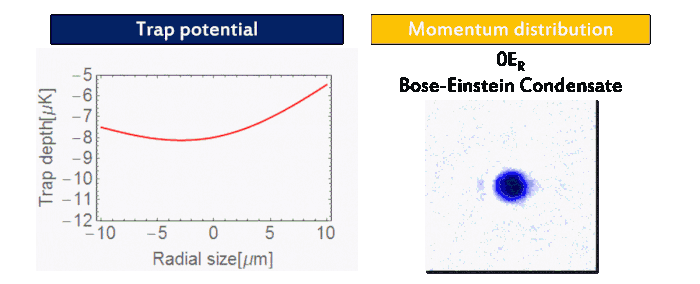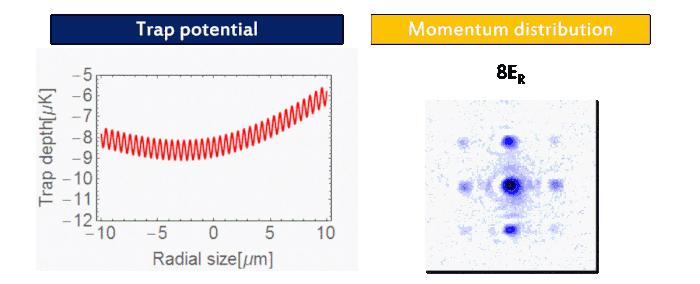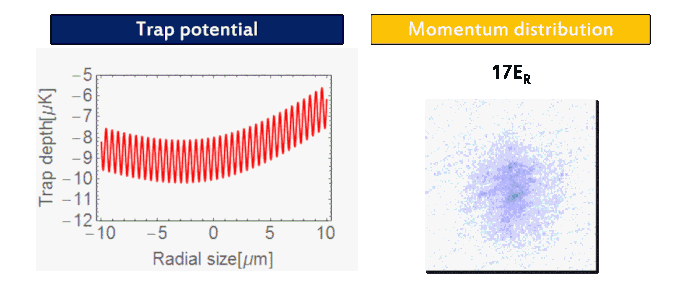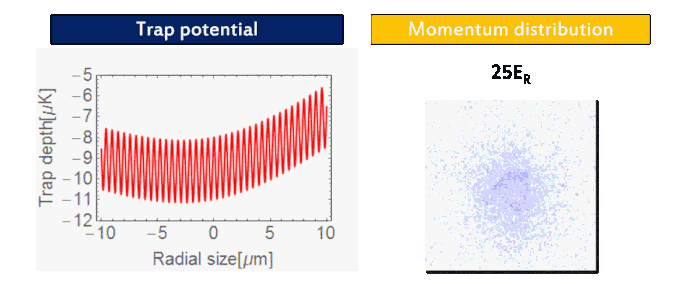
| Figure 3: Superfluid-Mott insulator transition. |
Results:
Figures 4 (b) and (c) show that the total atom number decays bi-exponentially when N = 74000 and 46000. The faster decay (time constant: ~1-2 ms) is due to the light-assisted collisions in multiply-occupied sites, whereas the slower one is due to the light-scattering loss (time constant: ~30-40 ms). In Fig. 4 (d), the faster decay disappears when N is decreased to 32000, and only the slower decay remains, demonstrating the absence of multiply-occupied sites, and therefore the generation of a unit-filling Mott insulator. This is consistent with the fact that lower number of atoms as well as weaker external trap-confinement are in general preferable for yielding a unit filling Mott insulator. Note that the lifetime of atoms in an optical lattice without MOT beams is dominated by collisions with a background gas, and is much longer than these decays seen in Figs. 4 (b)-(d). We have also calculated the atom number in each site from the number of atoms and external trap frequencies. This calculation also supports the demonstration of a unit filling Mott insulator under the experimental condition that gives the results shown in Fig. 4(d).
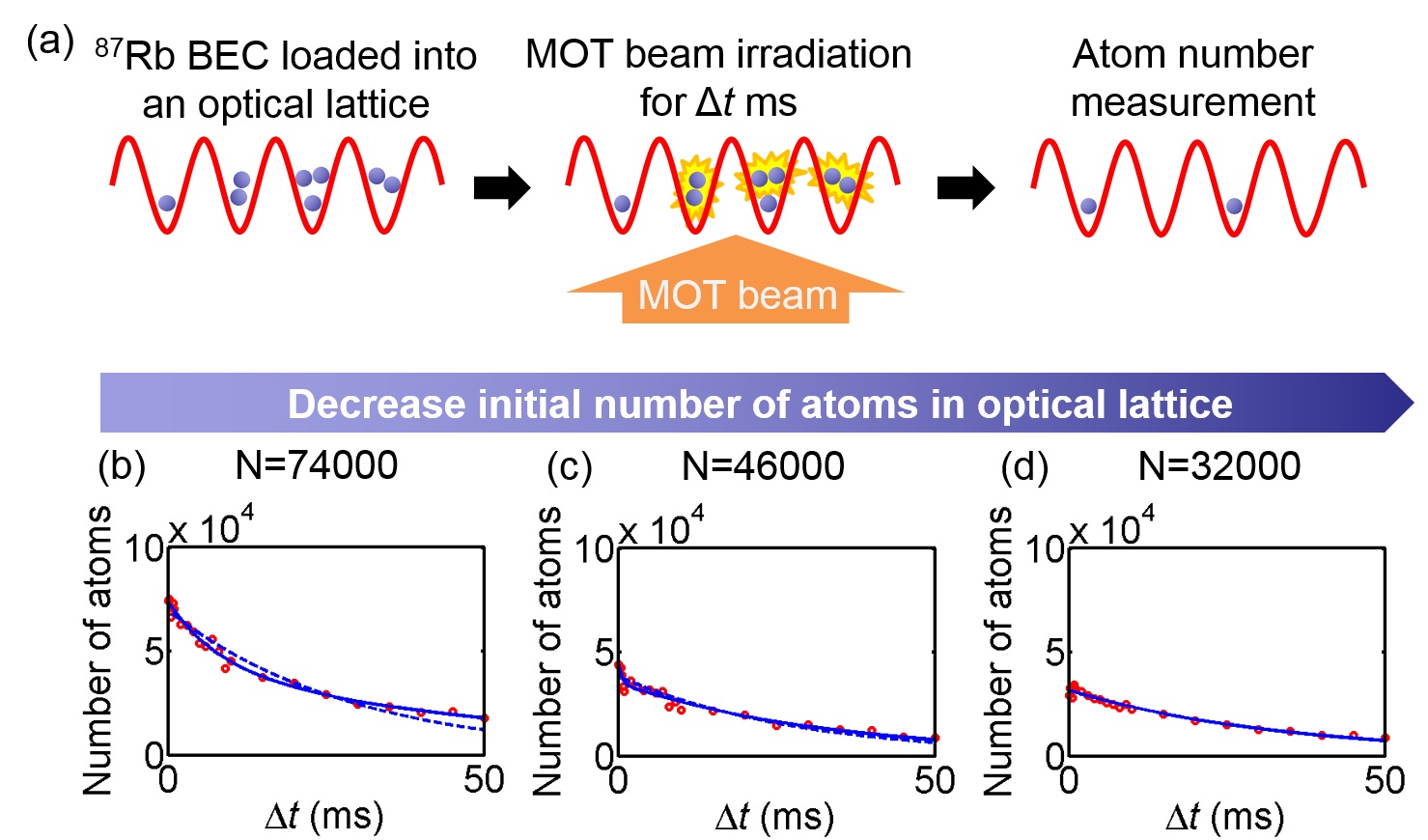
| Figure 4: (a) Measurement procedure of the atom number in each site in the Mott insulating phase. (b-d) Decay of the total atom number in an optical lattice during the irradiation of magneto-optical trap (MOT) beams. The initial total number N of atoms in the lattice is different among (b)-(d). Data points (red circles) are fitted with a sum of two exponential decays (blue line) or a single exponential decay (blue dotted line). |
Posted: 28 December 2016
First observation: 18 August 2016








