SAC/SAC-CI in PCM:励起状態の溶媒効果
PCM (polarizable continuum model)では、溶媒等の周囲の効果を、分極する誘電体でモデル化し、分子形状に合わせた空洞(cavity)表面の形式電荷として計算します。我々は、SAC/SAC-CI法とPCMを組み合わせた方法を開発しました。[JCP 2010, JCP 2011] SAC/SAC-CIのような非変分法に、周囲の効果を矛盾無く取り込む方法は、これまであまり研究されていませんでした。この方法は、溶質分子の電子状態の変化に応答した、溶媒の分極を取り込むことができます。また、溶媒の分極には、古典的モデルでは無視される「溶媒の電子状態」に起因する項を含めることができ、溶媒の分極の緩和を、速い項と遅い項に分けて、「非平衡溶媒和」の効果を考慮できます。
SAC/SAC-CI in PCMでは、速いプロセスとして、励起スペクトルや発光スペクトルの溶媒シフトの研究や、遅いプロセスとして、溶媒中での励起状態の構造最適化等を行うことができます。
基底状態と励起状態で、双極子モーメントや電荷分布が異なる場合、溶質の電子状態に対する溶媒の応答は大変重要で、それを平衡で扱うか、非平衡で扱うかで結果は大きく異なります。
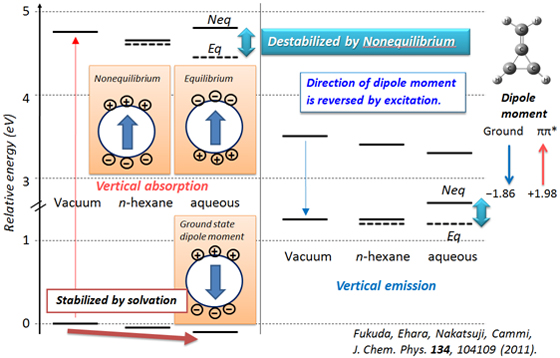
メチレンシクロプロペン(C4H4)の基底及び励起状態の相対エネルギー。吸光(absorption)は基底状態の最適化構造、発光(emission)は、励起状態の最適化構造で計算している。実線は非平衡溶媒和、破線は平衡溶媒和の結果を示している。
CAP/SAC-CI法:共鳴状態の理論
共鳴状態とは電子的に準安定な状態で、例えばN電子系基底状態よりもエネルギー的に不安定な(N+1)電子系の状態です。この共鳴状態を計算することができるCAP/SAC-CI法を、SAC-CI解で射影して計算する方法で開発しました。[CPL 2012]
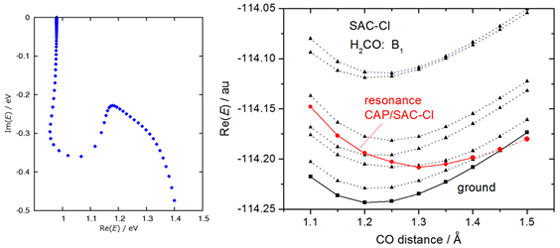
この方法をホルムアルデヒドのπ*共鳴状態に適用しました。CAP/SAC-CI 法によって得られたη-トラジェクトリを左図に示します。このトラジェクトリから共鳴状態のエネルギーや寿命が分かります。また得られた共鳴状態のポテンシャル曲線を右図に示します。電子付加した共鳴状態は基底状態よりも不安定であり、このように連続状態に埋もれた共鳴状態を計算することができます。
SAC-CI general-R 法:多電子過程の精密な理論 (1998-)
分子の励起状態には複雑な電子構造をもつ状態がありますが、励起状態の理論研究ではこれらを正確に求めることが重要になります。 複雑な電子状態にも高精度な理論SAC-CI general-R法[Nakatsuji, 1991]を開発し、極めて精度の高い研究を可能にしました。[CPL 1998] またこの理論によって励起状態の安定構造を探索するエネルギー・グラジエント法を開発しました。[JCP 2004]

Active space SAC-CI法:多電子過程の高精度・高効率な理論 (2007-)
SAC-CI general-R 法は多電子過程の状態の高精度計算に有用な方法であり、開殻電子系の励起状態に適用することができます。しかし、この方法では計算コストが高くなります。我々は、多電子過程を高精度かつ高効率に計算することができるActive space SAC-CI法を開発しました。[JCP 2007, MP 2009, TCA 2012] この方法では、高次の励起演算子は活性空間(active space)の軌道を含む励起演算子に限定します。
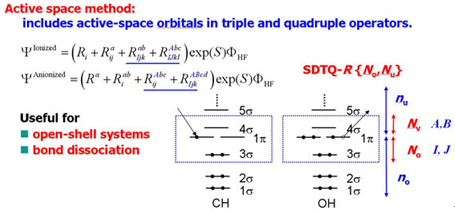
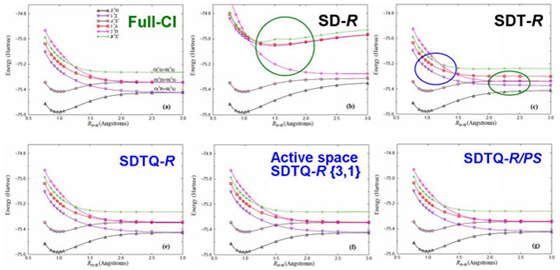
このActive space法を開殻分子系であるCH, OH分子に適用しました。図はOH分子のポテンシャル曲線を比較したものです。SD-R法は平衡核間距離であっても高い励起状態には記述が不十分であり、SDT-R法は結合解離領域の記述が悪いことが分かります。SDTQ-R法やActive space法では、完全解(full-CI)を詳細に再現しています。