Ryoichi Fukuda
Profile

Ryoichi FUKUDA
Associate Professor,Center for the Promotion of Interdisciplinary Education and Research (C-PiER),
Elements Strategy Initiative for Catalysts and Batteries (ESICB),
Kyoto University
Office
Elements Strategy Initiative for Catalysts and Batteries, Kyoto University1-30 Goryo-Ohara, Nishikyo-ku, Kyoto 615-8245, Japan
TEL: +81-75-383-3036 FAX: +81-75-383-3047 E-mail: fukuda [at] esicb.kyoto-u.ac.jp
Curriculum vitae
B. S. at Kyoto University, Faculty of Engineering (1996)M. S. at Kyoto University, Graduate School of Engineering (1998)
Ph. D. at Kyoto University, Graduate School of Engineering (2003)
21 COE research fellow at Kyoto University (2003-2007)
Part-time lecturer at Nara University of Education (2005-2006)
Research leader at Quantum Chemistry Research Institute (QCRI) (2007-2009 Apr)
Assistant Professor at Institute for Molecular Science (2009 May-2016 Apr)
Associate Professor at Elements Strategy Initiative for Catalysts and Batteries, Kyoto University (2016 May-)
Recent publications
-
Diels-Alder Cycloaddition of Cyclopentadiene and C60 at the Extreme High Pressure
T. Yang, R. Fukuda, R. Cammi, M. Ehara J. Phys. Chem. A 121, 4363-4371 (2017) DOI: 10.1021/acs.jpca.7b02805 -
Core-Shell vs. Other Structures in Binary Cu38-nMn Nanocluster (M = Ru, Rh, Pd, Ag, Os, Ir, Pt, and Au; n = 1, 2, and 6): Theoretical Insight into Determining Factors
N. Takagi, K. Ishimura, M. Matsui, R. Fukuda, M. Ehara, S. Sakaki J. Phys. Chem. C 121, 10514-10528 (2017) DOI: 10.1021/acs.jpcc.6b13086 -
Comparing the Performance of TD-DFT and SAC-CI Methods in the Description of Excited States Potential Energy Surface: an Excited State Proton Transfer Reaction as Case Study
M. Savarese, U. Raucci, R. Fukuda, C. Adamo, M. Ehara, N. Rega, I. Ciofini J. Comput. Chem. 38, 1084-1092 (2017) DOI: 10.1002/jcc.24780 -
A Theoretical Investigation on CO Oxidation by Single-Atom Catalysts M1/γ-Al2O3 (M = Pd, Fe, Co, and Ni)
T. Yang, R. Fukuda, S. Hosokawa, T. Tanaka, S. Sakaki, M. Ehara ChemCatChem 9, 1222-1229 (2017) DOI: 10.1002/cctc.201601713 -
Structures of bimetallic copper-ruthenium nanoparticles: incoherent interface and surface active sites for catalytic nitric oxide dissociation
R. Fukuda, N. Takagi, S. Sakaki, M. Ehara J. Phys. Chem. C 121, 300-307 (2017) DOI: 10.1021/acs.jpcc.6b09280 -
Electronic Transitions in Confomationally Controlled Peralkylated Hexasilanes
Y. Kanazawa, H. Tsuji, M. Ehara, R. Fukuda, D. L. Casher, K. Tamao, H. Nakatsuji, J. Michl, ChemPhysChem 19, 3010-3022 (2016) DOI: 10.1016/j.chemphys.2016.09.033 -
Electronic excitation and ionization behavior of N-hydroxypyridine-2(1H)-thione and its deprotonated anion in a polarizable medium studied using quantum chemical computations
R. Fukuda, and M. Ehara Theor. Chem. Acc. 135, 105 (9 pages) (2016) DOI: 10.1007/s00214-016-1870-4 -
Projected CAP/SAC -CI method with smooth Voronoi potential for calculating resonance states
M. Ehara, R. Fukuda, and T. Sommerfeld J. Comput. Chem. 37, 242-249 (2016) DOI: 10.1002/jcc.24010
Research interest
Direct SAC-CI Method
The SAC (symmetry-adapted cluster) and SAC-CI (configuration interaction) method is an accurate wavefunction theory for ground and excited states of molecules based on the coupled-cluster method.[1-5] The SAC-CI program has been released on Gaussian 03 and 09 programs.

- Cluster Expansion of the Wavefunction. Pseudo-Orbital Theory Applied to Spin Correlation, H. Nakatsuji and K. Hirao, Chem. Phys. Lett. 47, 569-571 (1977).
- Cluster Expansion of the Wavefunction. Symmetry-Adapted-Cluster (SAC) Expansion, Its Variational Determination, and Extension of Open-Shell Orbital Theory, H. Nakatsuji and K. Hirao, J. Chem. Phys. 68, 2053-2065 (1978)
- Cluster Expansion of the Wavefunction. Excited States, H. Nakatsuji, Chem. Phys. Lett. 59, 362-364 (1978).
- Cluster Expansion of the Wavefunction. Electron Correlations in Ground and Excited States by SAC (Symmetry-Adapted-Cluster) and SAC-CI Theories, H. Nakatsuji, Chem. Phys. Lett. 67, 329-333 (1979).
- Cluster Expansion of the Wavefunction. Calculation of Electron Correlations in Ground and Excited States by SAC and SAC-CI Theories, H. Nakatsuji, Chem. Phys. Lett. 67, 334-342 (1979).
- Formulation and implementation of direct algorithm for the symmetry adapted cluster and symmetry adapted cluster-configuration interaction method, R. Fukuda and H. Nakatsuji, J. Chem. Phys. 128, 094105 (2008)
- The SAC-CI website: http://www.qcri.or.jp/sacci/
SAC-CI Method in PCM
The SAC/SAC-CI method is combined to the PCM (polarizable continuum model)[1,2] to consider the solvent and other environmental effects on the electronic excitations. In this PCM SAC-CI method,[3,4] the solvent effects are considered self-consistently for every ground and excited states. This is the state-specific (SS) solvation scheme that is distinguished from the linear-response (LR) solvation scheme.[5,6] The SS scheme is essential for describing the photoemission processes.[7]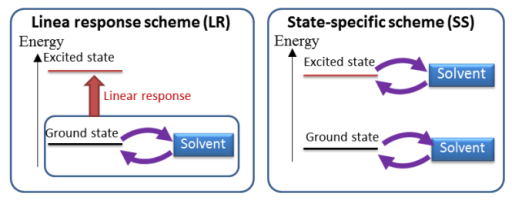
- Electrostatic interaction of a solute with a continuum. A direct utilizaion of ab initio molecular potentials for the prevision of solvent effects, S. Miertuš, E. Scrocco, and J. Tomasi, Chem. Phys. 55, 117-129 (1981).
- Quantum Mechanical Continuum Solvation Models, J. Tomasi, B. Mennucci, and R. Cammi, Chem. Rev. 105, 2999-3093 (2005).
- Symmetry-adapted cluster and symmetry-adapted cluster-configuration interaction method in the polarizable continuum model: Theory of the solvent effect on the electronic excitation of molecules in solution, R. Cammi, R. Fukuda, M. Ehara, and H. Nakatsuji, J. Chem. Phys. 133, 024104 (2010).
- Nonequilibrium solvation for vertical photoemission and photoabsorption processes using the symmetry-adapted cluster-configuration interaction method in the polarizable continuum model, R. Fukuda, M. Ehara, H. Nakatsuji, and R. Cammi, J. Chem. Phys. 134, 104109 (2011).
- Electronic excitation energies of molecules in solution: State specific and linear response methods for nonequilibrium continuum solvation models, R. Cammi, S. Corni, B. Mennucci, and J. Tomasi, J. Chem. Phys. 122, 104513 (2005).
- Electronic excitation energies of molecules in solution within continuum solvation models: Investigating the discrepancy between state-specific and linear-response methods, S. Corni, R. Cammi, B. Mennucci, and J. Tomasi, J. Chem. Phys. 123, 134512 (2005).
- Optical absorption and fluorescence of PRODAN in solution: Quantum chemical study based on the symmetry-adapted cluster-configuration interaction method, R. Fukuda, R. Chidthong, R. Cammi, and M. Ehara Chem. Phys. Lett. 552, 53-57 (2012).
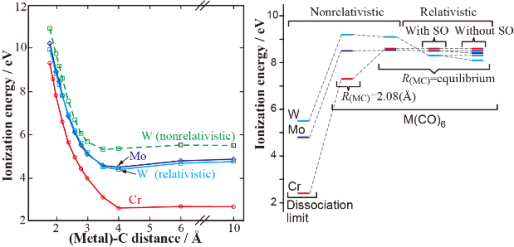
Relativistic Quantum Chemistry - consistent theory for all the elements in the periodic table
Chemistry deals with various combinations of more-than-one-hundred elements in the Periodic Table. We intend to find out the general laws of nature from such an infinite combination. Quantum chemistry has been playing a great role for a long time and it would play the leading role in science because it has been founded on the rigid physical principle.
-
Quasi-relativistic theory for the magnetic shielding constants. I. Formulation of Douglas-Kroll- Hess transformation for the magnetic field and its application to atomic systems, R. Fukuda, M. Hada, and H. Nakatsuji,
J. Chem. Phys. 118, 1015-1026 (2003)
-
Quasi-relativistic theory for the magnetic shielding constants. II. Gauge-including atomic orbitals and applications to molecules, R. Fukuda, M. Hada, and H. Nakatsuji,
J. Chem. Phys. 118, 1027-1035 (2003)
- Quasirelativistic theory for the magnetic shielding constant. III. Quasirelativistic second-order Moller-Plesset perturbation theory and its application to tellurium compounds, R. Fukuda and H. Nakatsuji, J. Chem. Phys. 123, 044101 (2005)
- Valence ionization spectra of group six metal hexacarbonyls studied by the symmetry-adapted cluster-configuration interaction method, R. Fukuda, S. Hayaki, and H. Nakatsuji, J. Chem. Phys. 131, 174303 (2009)
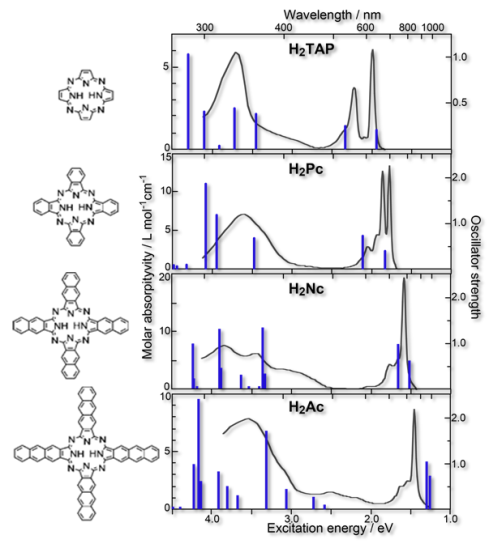
Electronic Excited States of Large Conjugated Molecules
Performing reliable calculations for the electronic excited states of large conjugated molecules is a challenging subject in computational quantum chemistry. The direct SAC-CI method[1] is an appropriate method for studying the excited states of large systems because[2]Many excited states of large conjugated molecules can be calculated by the direct SAC-CI method within moderate computational costs and reasonable accuracy.

- Formulation and implementation of direct algorithm for the symmetry adapted cluster and symmetry adapted cluster-configuration interaction method, R. Fukuda and H. Nakatsuji, J. Chem. Phys. 128, 094105 (2008)
- Symmetry-adapted-cluster/symmetry-adapted-cluster configuration interaction methodology extended to giant molecular systems: Ring molecular crystals, H. Nakatsuji, T. Miyahara, R. Fukuda, J. Chem. Phys. 126, 084104 (2007)
- Excited states and electronic spectra of extended tetraazaporphyrins, R. Fukuda, M. Ehara, and H. Nakatsuji, J. Chem. Phys. 133, 144316 (2010)
- Excited states and electronic spectra of annulated dinuclear free-base phthalocyanines: a theoretical study on near-IR-absorbing dyes, R. Fukuda and M. Ehara J. Chem. Phys. 136, 114304 (2012)
- Theoretical study on the excited electronic states of coronene and its π-extended molecules using the symmetry-adapted cluster-configuration interaction method, R. Fukuda and M. Ehara Bull. Chem. Soc. Jpn. 86, 445-451 (2013)
- Electronic excitations of C60 fullerene calculated using the ab initio cluster expansion method, R. Fukuda and M. Ehara J. Chem. Phys. 137, 134304 (2012)
Molecular Interactions in Excited States and Solvatochromism
The difference between the transition energy of a dye molecule in a solvent and that in the gas phase is known as the solvatochromic shift. This shift reflects the interaction between the dye molecule (solute) and its solvent environment. The solvatochromism is also important for biological probes such as fluorescence imaging because molecular probes can detect the polarization of environment. We have developed the PCM (polarizable continuum model) in the SAC-CI framework for studying the solvent effects on electronic excited states.[1,2] The PCM SAC-CI has been applied to the solvatochromism of transition metal complexes that involve various types of electronic excitations that show distinctive solvent dependence.[3]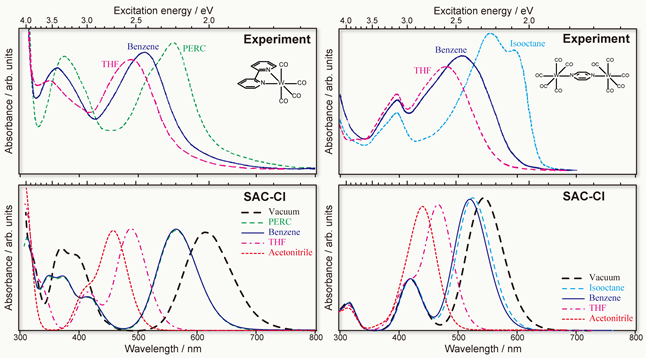
We are also studying the dispersion interaction (van der Waals force) in excited states that is an important origin of the solvatochromic shift for large conjugated molecules in nonpolar solvents.[4] Since the SAC-CI is a many-body wavefunction theory, it can describe the dispersion interactions both in the ground and excited states. The van der Waals interactions in the electronically excited porphyrins were studied with using the SAC-CI method.[4,5]
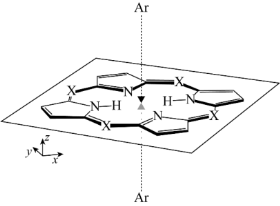
- Symmetry-adapted cluster and symmetry-adapted cluster-configuration interaction method in the polarizable continuum model: Theory of the solvent effect on the electronic excitation of molecules in solution, R. Cammi, R. Fukuda, M. Ehara, and H. Nakatsuji, J. Chem. Phys. 133, 024104 (2010).
- Nonequilibrium solvation for vertical photoemission and photoabsorption processes using the symmetry-adapted cluster-configuration interaction method in the polarizable continuum model, R. Fukuda, M. Ehara, H. Nakatsuji, and R. Cammi, J. Chem. Phys. 134, 104109 (2011).
- Electronic excitation spectra of molecules in solution calculated using the symmetry-adapted cluster-configuration interaction method in the polarizable continuum model with perturbative approach, R. Fukuda, M. Ehara, and R. Cammi J. Chem. Phys. 140, 064114 (2014)
- Mechanisms for solvatochromic shifts of free-base porphine studied with polarizable continuum models and explicit solute-solvent interactions, R. Fukuda and M. Ehara J. Chem. Theory Comput. 9, 470-480 (2013)
- Theoretical study of the electronic excitations of free-base porphyrin-Ar2 van der Waals complexes, R. Fukuda and M. Ehara J. Chem. Phys. 139, 074303 (2013)